SciPy函数库在NumPy库的基础上增加了众多的数学、科学以及工程计算中常用的库函数。例如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等。
最小二乘拟合
假设有一组实验数据(x[i],y[i]),我们知道他们之间的函数关系:y=f(x),通过这些已知信息,需要确定函数中的一些参数项。例如:如果f是一个线形函数f(x)=k*x+b,那么参数k和b就是我们需要确定的值。如果将这些参数用p表示的话,那么我们就要找到一组p值使得如下公式的S函数最小:
其中y为原函数,f为拟合函数。拟合函数可通过给定值找出表达式,不要求多精确,之要求能反映数据变化的趋势。
这种算法被称为最小二乘拟合。
scipy中的子函数库optimize已经提供了实现最小二乘拟合算法的函数leastsq。
#-*- coding: utf-8 -*- import numpy as np
A,k,theta=p def residuals(p,y,x): return y-func(x,p) #在0~-2*np.pi均匀返回100个数字 A,k,theta=10,0.34,np.pi/6 #真实数据的函数参数 p0=[7,0.2,0] #第一次猜测的函数拟合参数 #调用leastsq进行数据拟合 print("Real_parameter:",[A,k,theta])
pl.plot(x,y0,label="RealData") pl.legend() |
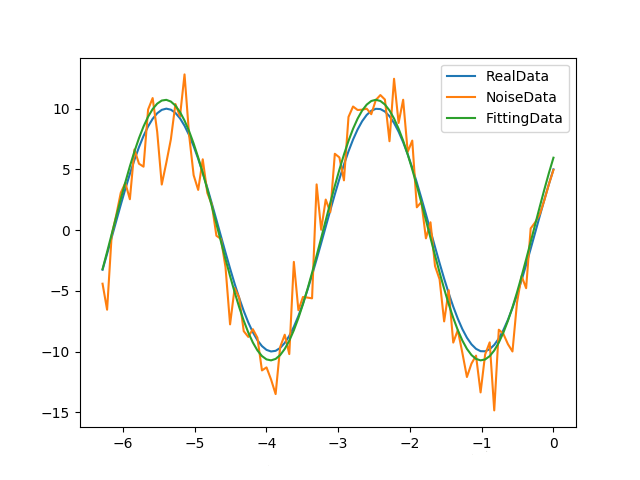
这里我们要拟合的函数是一个正弦波函数,它有参个参数A,k,theta分别对应振幅,频率,相角。假设实验数据是一组包含噪声的数据x,y1,其中y1是在真实数据的基础上加入噪声得到的。
通过leastsq函数对带噪声的实验数据x,y1进行数据拟合,可以找到x和真实数据y0之间的正弦关系的参数:A,k,theta。
Real_parameter: [10, 0.34, 0.5235987755982988] |
函数最小值
optimize库提供了几个求函数最小值的算法:fmin,fmin_powell,fmin_cg,fim_bfgs。下面的程序通过求解卷积的逆运算岩石fmin的功能。
对于一个离散的线性时不变系统h,如果他的输入是x,那么其输出也可以用x和h卷积表示,即y=x*h。
现在的问题是如果已知系统的输入x和输出y,如何计算系统的传递函数h;或者如果已知系统的传递函数h和系统的输出y,如何计算系统的输入x。这种运算被称为反卷积运算。
#coding:utf-8 import scipy.optimize as opt
def convolve_func(h): #调用fmin函数,以x0为初始值 print(fminfunc.__name__) #输出x(*)h0和y之间的相对误差 #输出h0和h之间的相对误差 def test_n(m,n,nscale): x=np.random.rand(m) yn=y+np.random.rand(len(y))*nscale test_fmin_convolve(opt.fmin,x,h,y,yn,x0) if __name__=="__main__": |
fmin |
非线性方程组求解
optimize库中的fsolve函数可以用来对非线性方程组进行进行求解。
func(x)是计算方程组误差的函数,它的参数x是一个矢量,表示方程组的各个未知数的一组可能解,func返回将x带入方程组之后得到的误差;x0为未知数矢量的初始值。
实例:
求解
5*x1+3=0
4x0x0-2sin(x1x2)=0
x1*x2-1.5=0
#coding:utf-8
def f(x): result=fsolve(f,[1,1,1]) #输入一组可能解 print(result) |
[-0.70622057 -0.6 -2.5 ] |
在对方程组进行求解时,fsolve会自动计算方程组的雅可比矩阵,如果方程组中的未知数很多,而与每个方程有关的未知数较少时,传递一个计算雅可比矩阵的函数将能大幅度提高运算速度。
什么是雅可比矩阵?
雅可比矩阵是一阶偏导数以一定方式排列的矩阵,它给出可微分方程与给定点的最优线性逼近,因此类似于多元函数的导数。
使用雅可比矩阵的fsolve,计算雅可比矩阵的函数j通过fprime参数传递给fsolve,函数j和函数f一样,有一个未知数的解矢量参数x,函数j计算非线性方程组在矢量x点上的雅可比矩阵。
#coding:utf-8 from scipy.optimize import fsolve
def f(x): def j(x): #求每个方程的偏导数,生成雅可比矩阵 print(result) |
运行可以感觉到效率明显提高。
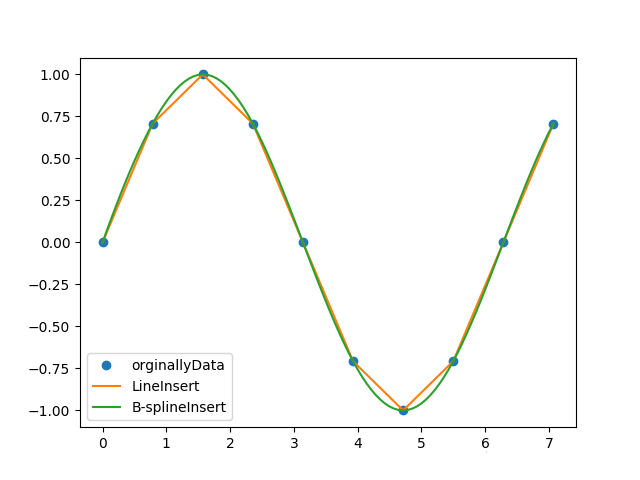
interpolate库提供了许多对数据进行插值运算的函数。下面使用直线和B-Spline对正弦波上的点进行插值。
#coding:utf-8 import numpy as np plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
x_new=np.linspace(0,2*np.pi+np.pi/4,100) #得到一个新的线性插值函数 #计算出B-Spline曲线的参数 #将参数传递给splev函数计算出各个取样点的插值结果
pl.legend() |
数值积分是对定积分的数值求解,例如可以利用数值积分计算某个形状的面积。
实例:
计算半径为1的半圆的面积。
单位半圆曲线可以用下面函数表示。
#coding:utf-8 def half_circle(x):
N=1000 #使用分割法计算 #进行数值积分
pi_half,err=integrate.quad(half_circle,-1,1)
|
Split_run: 3.138345831727239 |
可以看出quad函数是非常精确的。
多重定积分的求值可以通过多次调用quad函数实现,为了方便,integrate库提供了dblquad函数进行二重积分,tplquad函数进行三重积分。
实例:
计算单位半球体积。
符合x**2+y**2+z**2=1
from scipy import integrate def half_circle(x): def half_sphere(x,y): # X-Y轴平面与此球体交线为一个单位圆,因此积分区间为此单位圆,可以考虑 V=integrate.dblquad(half_sphere,-1,1, print(V) #通过球体体积公式计算 |
(2.0943951023931984, 1.0002354500215915e-09) |
dblquad函数的调用方式:
dblquad(func2d,a,b,gfun,hfun) |
对于func2d(x,y)函数进行二重积分,其中a,b为变量x的积分期间。
scipy.integrate库提供了数值积分和常微分方程组求解算法odeint。
实例:
计算洛伦兹吸引子的轨迹,洛伦兹吸引子有三个微分方程定义:
dx/dt=σ(y-x) |
这三个方程定义了三维空间中各个坐标点上的速度矢量。从某个坐标开始沿着速度矢量进行积分,就可以计算出无质量点在此空间中的运动轨迹。其中 σ, ρ, β 为三个常数,不同的参数可以计算出不同的
运动轨迹: x(t), y(t), z(t)。 当参数为某些值时,轨迹出现馄饨现象:即微小的初值差别也会显著地影响运动轨迹。下面是洛仑兹吸引子的轨迹计算和绘制程序:
#coding:utf-8
x,y,z=w #直接用lorenz的计算公式对应 return np.array([p*(y-x),x*(r-z)-y,x*y-b*z])
#调用ode对lorenz进行求解,用两个不同的初始值
plt.show() |

在程序中先定义一个lozren函数,它的任务是计算出某个位置的各个方向的微分值,这个计算直接根据洛伦兹吸引子公式得出。但后调用odeint,对微分方程求解:
参数祥解:
lorenz:计算某个位移上的各个方向的速度;
(0.0,1.0,0.0),位移初始值。计算常微分方程所需的各个变量的初始值。
t:表示时间的数组,odeint对于此数组中的每个时间点进行求解,的出所有时间点的位置。
args:这些参数直接传递给lorenz函数,因此他们都是常量。
滤波器设计
scipy.signal库提供了西多信号处理反面的函数。如何利用signal库设计滤波器,查看滤波器的频率响应,以及如何使用滤波器对信号进行滤波。
设计一个带通滤波器:
import scipy.signal as signal b,a=signal.iirdesign([0.2,0.5],[0.1,0.6],2,40)
|
通过调用freqz计算所得到的滤波器的频率响应:
w,h=signal.freqz(b,a) |
frez返回两个数组w和h,其中w是圆频率数组,通过w/pi*f0可以计算出其对应的实际频率.h是w中的对应频率点的响应.其幅值为滤波器的增益,相角为滤波器的相位特性.
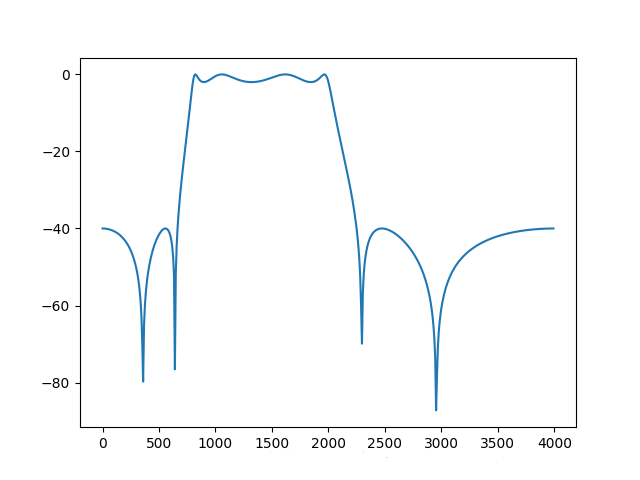
计算h的增益特性,并转换为dB度量,由于h中存在幅值几乎为0的值,因此先用clip函数对其进行裁剪,在调用对数函数,避免计算出错。
#绘制出滤波器的增益特性图 pl.show() |
测量未知系统的频率特性
将频率扫描到系统中,观察系统的输出,从而计算其频率特性。
# 为了调用chirp函数产生频率扫描波形的数据,首先产生一个等差数组代表取样时间, #调用chirp得到2秒钟的频率扫描波形数据 #调用lfilter函数计算sweep波形经过带通滤波器值后的效果 |
lfilter内部通过如下算是计算IIR滤波器的输出:
数组x代表输入信号,y代表输出信号:
y[n]=b[0]x[n]+b[1]x[n-1]+...+b[P]x[n-P] |
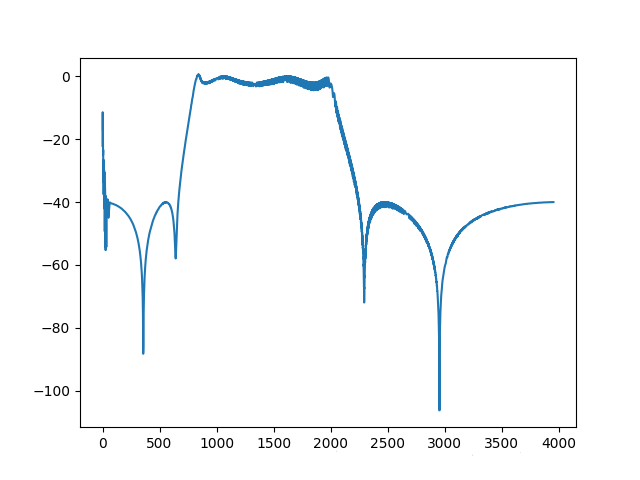
获取输出波形的包络,所以先将输出波形数据转换为能量值:
# 为了调用chirp函数产生频率扫描波形的数据,首先产生一个等差数组代表取样时间, #调用chirp得到2秒钟的频率扫描波形数据 #调用lfilter函数计算sweep波形经过带通滤波器值后的效果
#找到所有能量大于前后两个取样点的下标 #将时间转换为对用频率,绘制所有局部最大点的能量值: pl.show() |
用Weave嵌入C语言
Python作为动态语言其功能虽然强大,但是在数值计算方面有一个最大的缺点:速度不够快。在Python级别的循环和计算的速度只有C语言程序的百分之一。因此才有了NumPy, SciPy这样的函数库,将高度优化的C、Fortran的函数库进行包装,以供Python程序调用。如果这些高度优化的函数库无法实现我们的算法,必须从头开始写循环、计算的话,那么用Python来做显然是不合适的。因此SciPy提供了快速调用C++语言程序的方法-- Weave。